PITÀGORES: LA MÚSICA I LES MATEMÀTIQUES

En aquest àudio s’explica la historia de com Pitàgores aconsegueix relacionar la música amb les matemàtiques.

EL NOMBRE CLAU

Aquest vídeo que us deixo esta tot molt ben explicat sobre el nombre phi. Crec que us pot ajudar a entendre millor el que he anat explicant fins ara d'una manera visual.

IMATGES ESPECTACULARS

Aquí veureu una introducció amb unes gràfiques espectaculars de la seqüència de Fibonacci, la proporció àuria i com ho trobem a la natura.

TAMBÉ EN LA MÚSICA

També el disseny aplicat als instruments musicals pot tenir relació àuria. El prominent lutiher Antonio Stradivarius (1644-1737) hi posava molta cura a l'hora de situar els forats dels seus violins en proporció àuria. Malgrat el rigor de l'italià, no hi ha cap evidencia de la influencia de la col·locació amb la qualitat del só. Sembla que alguns compositors (sobretot del post-romanticisme i impressionisme), com Debussy i Béla Bartók coneixien i feien servir en les seves partitures la proporció àuria, que era en el punt culminant de la peça.
 

CONSTRUCCIÓ D’UN RECTANGLE AURI

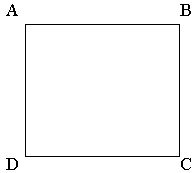
Partim d’un quadrat ABCD, que el seu costat serà el menor del RA que construirem:

1. Tracem la mediatriu al segment AB que ens dona el punt M.
2. Amb centre a M i radi MC tracem un arc que talla la prolongació AB, això ens dona el E.
3. Tracem una perpendicular des de E que talli a F.

Així aconseguim el rectangle ADEF, que sens dubte és un RA (rectangle auri).

RESUM DEL TEOREMA DE PITÀGORES

Quan els valors dels costats d’un triangle rectangle són nombres enters, formen un conjunt de tres nombres que s’han denominat terna pitagòrica.

a2 = b2 + c2

Amb la successió de Fibonacci podem trobar ternes pitagòriques. Escollim quatre termes qualsevol però consecutius de la successió, com per exemple 2, 3, 5 i 8.

Amb ells formem tres nombres:

1.      El producte dels extrems: 2 · 8 = 16

2.      El doble del producte dels centrals: 2(3·5) = 30

3.      La suma dels quadrats dels dos centrals: 3² + 5² = 34

Podem comprovar que aquets tres numeros (34, 30, 16) formen una terna pitagòrica

           
            16² =   256

            30² =   900

      +_____

34² = 1156

UN MÓN AURI

Una manera tradicional de representar la proporció àuria és: una recta està dividida en mitja i extrema raó. Quan la longitud de la línea total és a la part major, com la de aquesta part major és a la de la menor, es a dir, que el tot és a la part com la part al resta.

En les carteres i les bosses dels ciutadans moderns s’acumulen documents identificatius i targetes de tot tipus: targetes de crèdit, carnets de biblioteques, piscines...
Els traiem i els tornem a guardar a diari sense prestar al fet que la majoria de les targetes guarden la mateixa proporció que la de un rectangle auri.

Quan posem dos targetes iguals en aquesta posició, i tracem una diagonal en la primera de un dels seus vèrtexs a un altre i coincideix amb el vèrtex de la segona, les dos targetes són de proporció àuria. 

Com ja sabem, un rectangle és auri quan la relació entre els seus costats és phi. D'ara endavant, direm els rectangles auris per les seves inicials RA.